 Accueil
Accueil 
 Forum
Forum 
 Mail
Mail
Définir une suite réelle u, c'est associer à tout entier réel n, un nombre réel noté un
u : N -> ROn dit que un est le terme général de la suite
Pour tout entier n, un est le terme d'indice n où le terme de rang n.
Une suite peut être définie pour tout entier n supérieur à p:
Pour n supérieur ou égal a p, on a : u: n -> un
On appelle p le terme initiale de la suite. On dit que la suite est définie à partir du rang p .
Comme vous l'avez remarquer, une suite ressemble beaucoup à une fonction, la différence majeure étant qu'une suite ne prend que des entiers naturels comme inconnus en effet, n appartient toujours à N alors que x (dans une fonction appartient a R.
ce qui fait q'une suite u se note aussi (un)
Le terme général un de la suite (un) est exprimé en fonction de n, c'est à dire indépendamment des termes précédents. En claire, il n'existe pas de relation directe entre (un) et (un+1).
Bon là le lien avec les fonction n'est pas trop dure à faire!
Soit C la courbe représentative de f sur [0 ; +∞[, les termes un de la suite (un) sont les ordonnées des points de C qui ont des abscisses entières.
TAJI, si tu le dis........ je te crois.... mais ne me demande pas de te suivre.... bon ok, voila un petit schéma qui comme toujours tombe à point nommé...
 |
Je vais commencer par vous expliquer ce qu'est la récurrence, (étant donné que je prépare mon bac de français.... j'en profite...). Bon, on appelle un phénomène récurent, un phénomène qui revient de façon régulière, voir systématique.... Ainsi, comme vous l'avez tous constaté, les devoirs sont récurrents.... bon je pense que là tout le monde voit à peu près de quoi je veux parler!
En appliquant cette définition, on dit qu'une suite (un est récurrente quand elle est définie par son terme initial et par une relation (toujours la même!!!) de récurrence, c'est à dire pour parler français que chaque terme est donné en fonction du terme qui le précède.
On dit que un est définie par récurrence, ou que un est une suite récurrente associée à f.
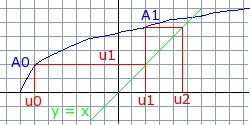
Soit C, la courbe représentative de f, A0 est le point d'abscisse u0 et d'ordonnée u1
=f(u0), les termes un sont disposés sur l'axe des abscisses.
Pour placer ces points, on se sert de la droite d'équation y = x, comme le montre le schéma:
 |
Là, il n'y a rien à ajouter, si ce n'est que cela ressemble quand même pas mal aux variations d'une fonction. La seule manière de retenir de façon intelligente ces propriétés est de les essayer sur un maximum d'exemple pour comprendre....
Ainsi, pour étudier le sens de variation d'une suite, on peut:
Soit p un entier naturel non nul, La suite un est périodique, et de période t si quel que soit n, on a :
un+1 = un.
Comme vous le constater, cette partie est en tout point comparable à la périodicité des fonction . Pour ceux qui auraient zapper un de mes chapitre, rdv ici
Encore une fois c'est par pure formalité que je fais cette partie, car tout a déjà été vu dans le premier chapitre d'algèbre....