Accueil Forum Mail Livre d'OR

Chapitres

NOTION DE CALCUL VECTORIEL

OK, c'est bon, tout le monde est là? alors je continue mon cour mais avant laissez moi vous dire que ne pouvant placer des "petites flèches" au dessus des vecteurs je placerai l'attribut C.S.S. overline c'est a dire que les vecteurs seront uniquement marqués d'une ligne au dessus

I- Vecteurs de l'espace

Caractérisation d'un vecteur

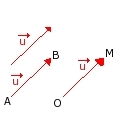
Soit un vecteur de l'espace non nul u = AB (avec A différent de B); alors: sa direction est celle de la droite (AB), attention toutefois a l'ordre des lettres! son sens est de A vers B sa norme, est la distance de A à B

remarque:
soit O un point de l'espace, et u un vecteur de l'espace, il n'existe qu'un seul point M tel que OM = u

égalité vectorielle

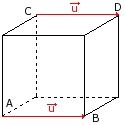
Dire que AB = CD signifie que ABCD est un parallélogramme, c'est à dire que les segments [AD] et [CD] ont le même milieu.

Bon je ne vais qu'effleurer la partie sur les additions vectorielles car vous savez tous qu'à ce sujet c(est toujours la relation de Chasles qui intervient et qui dit: AB+BC = AC Cela reste vrai dans l'espace!!!

règles de calculs

Pour trois vecteurs quelconques u, v et w de l'espace, on a:

• (u+v) + w = u +(v+w);
• u + v = v + u;
• u + 0 = u;
• tout vecteur u admet un opposé noté -u tel que u + (-u) = 0. Si u = AB, alors -u = BA.

multiplication d'un vecteur par un réel

Soit λ un réel non nul et u un vecteur de l'espace. Si u est différent de 0, alors, le vecteur λu est de vecteur: - qui a la même direction que u; - qui est de même sens que u si λ est strictement positif et de sens contraire si λ est strictement négatif; - ||λu|| =|λ||u|||.

règles de calculs

Et oui , tous les pretextes sont bons pour en rajouter une louche mais au fond, n'est-ce pas le but des maths que de faire faire des calculs?!

Pour tous les réels α et β et pour tous les vecteurs u et v de l'espace:

• α(u+v) = αu + αv
• (α+β)u = αu + βu
• α(βu) = (α&beta) u

II- Vecteurs colinéaires

Vecteurs colinéaires
Deux vecteurs u et v de l'espace sont colinéaires s'il existe trois points alignés A, B, et C tels que : u = AB et v = AC

Ce qui m'amène à vous dire que le vecteur nul est colinéaire à tous les vecteurs de l'espace en effet, les points A, A et C sont toujours alignés...

Caractérisation de la colinéarité
Soit u et v deux vecteurs non nuls de l'espace. les vecteurs u et v sont colinéaires si et seulement si, il existe un réel k tel que u = kv Il faut également qu'ils aient la même direction ...

Bon une petite pause et on repart, désolé, c'est pour ma tête à moi qui commence à faire mal....
aller c'est repartit...

Repère d'une droite
Un repère d'une droite D est un couple (A; u), où A est un point de la droite D et u est le vecteur directeur de la droite D. C'est à dire que u est un vecteur non nul mais qui a la même direction que la droite D.

On dit que tous les vecteurs non nuls et colinéaires au vecteur AB sont des vecteurs directeurs de la doite (AB).

III- vecteurs coplanaires

théorème
Soit un point A de l'espace et deux vecteurs u et v non colinéaires. L'ensemble P des points M de l'espace tels que : AM=αu+βv, avec α et β réels; est le plan du repère (A;u;v).

On dit que les réels α et β sont le couple de coordonnées du point M dans le repère (A;u;v).

voilà une comment on peut définir autrement la coplanarité (je ne sais pas si c'est comme ça qu'on dit?) de deux vecteurs.

Trois vecteurs u; v et w de l'espace sont coplanaires s'il existe des points A, B, Cet D coplanaires tels que u=AB, v = AC et w= AD

Caractérisation de la coplanarité
Soit u; v et w trois vecteurs de l'espace (comme vous le constatez tous, je traverse une longue periode de non-inspiration pour nommer mes vecteurs), donc on a trois vecteurs u; v et w et en plus u et v ne sont pas colinéaires... Dans ce cas, on peut dire que les vecteurs u; v et w sont coplanaires s'il existe deux réels (encore mon inspiration...) α et β tels que: w = αu + βv

IV- Repère de l'espace

1) Repère de l'espace

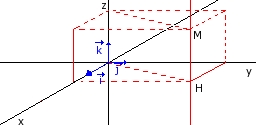
Si O est un point de l'espace et i, j et ktrois vecteur non coplanaires, alors pour tout point M de l'espace, il existe un unique triplet de réels (x; y; z) tels que: OM = xi + yj + zk. On dit que (x; y; z) est le triplet des coordonnées du point M dans le repère (O;i;j;k) de l'espace. x est l'abscisse de M, y est son ordonnée et z sa cote. On dit aussi que , y et z sont les coordonnées du vecteurs OM dans la base i;j;k Ce que l'on note OM(x;y;z).

Bon, je pense que là, il n' y rien ou pas grand chose que vous n'ayez vu dans les classes précédentes mais bon, les rappels ne peuvent pas vous faire de mal...

2) Repère particulier

• Si les vecteurs i = OI, j = OJ et k = OK sont orthogonaux deux à deux (c'est à dire que les droites (OI), (OJ) et (OK) sont orthogonales => cf chapitre précédent), on dit que le repère (O;i;j;k) est un repère orthogonal de l'espace

• Si de plus ||i|| = 1, ||j|| = 1 et ||k|| = 1; alors le repère(O;i;j;k) est un repère orthonormal de l'espace

  3) Calculs dans un repère

  théorème
  On travaille dans un repère (O;i;j;k) de l'espace. Si A(xA; yA; zA) et B(xB; yB; zB), alors AB (xB - xA; yB - yA; zB - zA). Si u(x;y;z) et v(x';y';z') alors u + v (x + x'; y + y'; z + z') et λu(λx; λy; λz) quel que soit le réels λ.

  4) Distance entre deux points

  théorème
  Soit (O;i;j;k) un repère de l'espace. Si A(xA; yA; zA) et B(xB; yB; zB), alors: AB = ||AB|| = -/(xB - xA)² + (yB - yA)² + (zB - zA)² Si u(x;y;z), alors ||u|| = -/x² + y² + z²

  Pour ceux qui cherche à prouver ce théorème (vous avez le droit d'être mazo après tout!), juste un conseil, faîtes un schéma et pensez à appliquer le théorème le plus connu du mon de, celui de Pythagore...

  page d'accueil>>Mathématiques>>géométrie>>>Calcul vectoriel