Chapitres

ANGLES ET TRIGONOMETRIE

I- Le cercle trigonométrique

Vous vous souvenez tous j'en suis persuadé, de ce chapitre déja vu en seconde et c'est avec un bonheur indicible que vous avez cliqué sur le lien pemettant d'accéder à cette page!!! non, je me trompe? Tant mieux mais je ne vous cache pas à quel point je deteste cette partie du programme de math mais bon, il faut faire avec...

Soit (O;OA;OB) un repère du plan,
Le cercle trigonométrique est le cercle de centre O et de rayon 1 sur lequel on a choisit un sens positif de parcours:par convention (c'est à dire que c'est comme ça, il ne faut pas discuter...) c'est le sen inverse des aiguilles d'une montre, soit une rotation de droite à gauche pour ceux qui n'ont pas de montre à aiguilles =>que voullez vous, je m'adapte... on appelle ce sens le sens direct, l'autre étant bien évidemment le sens indirecte.

pour ceux qui seraient un peu bouché ou un peu imperméable à ce que je raconte voilà un p'tit schéma qui résume un peu ce que je vient de dire Chaque point M du cercle C est repéré par un réel α; ce réel est la longueure de l'arc AM si M appartient au demi-cercle (ABA').

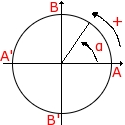ici, A' est repété par π B par π/2 et B' par -π /2.
le nombre &alpha est une mesure en radian de l'arc orienté AM ou de l'angle orienté (OA;OM)

Or la circonférence du cercle trigonométrique est exactement 2π donc pour atteindre M à partir de A, on peut effectuer un nombre entier de tours, dans un sens ou dans l'autre, puisqu'un tour vaut 2π.Ainsi l'angle orienté admet une infinité de mesures:
On écrit (OA;OM) = α + k2π, ou k appartient à Z
On peut aussi écrire (OA;OM) = α[2π] ce qui se lit α modulo 2π

La mesure qui est comprsie dans l'intervalle ]-π;π) est appelé la mesure principale de l'agle orienté

On dit que leplan est orienté si un cercle du plan est orienté, tous les cercles sont alors orientés dans le même sens, le repère est dit orthonormal directe

II- Angles orientés de deux vecteurs (non nuls)

Angles orientés de vecteur

définition

Soit u et v deux vecteurs non nuls et C le cercle trigonométrique de centre O. La demi-droite [O,m), de même direction et de même sens que le vecteur u coupe le cercle Cen un point M. La demi-droite [on) de même direction et de même sens que le vecteur v coupe le cercle C en N. Les mesures de l'angle orienté (u, v) sont les réel s - t où s et t sont des réels respectivement associés aux points N et M dans l'enroulement de la droite des réels autours de C.

Les mesures de l'angles orienté (u, v) ne dépendent ni du choix du point O ni du choix de l'origine A sur le cercle C.

Lien entre les mesures

Tout angle orienté admet une infinité de mesures.
Si &alpha est un mesure de la'angle orienté (u, v), alors les mesures de cet angle orienté sont les réels α + k2π, avec k appartient a Z, c'est à dire à l'ensemble des entiers relatifs.
On écrit: (u, v) = &alpha (2π) , et on lit l'angle orienté (u, v) a pour mesure α modulo 2 π