 Accueil
Accueil 
 Forum
Forum 
 Mail
Mail
| Soit un une suite numérique et l un nombre réel. La suite un converge vers L si tout intervalle ouvert contenant L contient aussi les termes de la suite un à partir d'un certain rang p. Dans ce cas, on dit que la suite un est convergente. |
pour n >ou= p un est dans l'intervalle: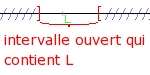 |
Si une suite un converge vers L, alors toutes les suites qui auront étés obtenues à partir de un, en modifiant un nombre fini de termes, convergent elles aussi vers L
Dire que la suite un converge vers L, revient à dire que la suite (un - L) converge vers 0.
| Limite d'une suite convergente |
|---|
| 1- Si (un) est une suite convergent, alors il existe un unique réel vers lequel elle converge. 2- L est la limite de la suite un. on note: limn->+∞un = L, ou encore, lim(un) = L |
remarques:
Si une suite convergente est monotone alors, tous les termes de cette suite seront situés du même coté de la droite d'équation y = L.
Sinon, si elle n'est pas monotone, alors: soit les termes un oscillent au-dessus et au-dessous de cette droite d'équation y = L, soit ces termes un ont du même coté de cette droite.... ça dépend alors d la suite.
une suite divergente est une suite qui n'est pas convergente. Il y a deux éventualités:
- Soit elle admet une limite infinie;
- soit elle n'a pas de limite.
Une suite numérique unadmet pour limite +∞ si tout intervalle ouvert de la forme ]a; +∞[ contient tous les termes de la suite à partir d'un certains rang p. ON note: limn->+∞ un = +∞ ou lim(un. |
un pour n > ou = p |
Il en va de même avec une suite qui admet -∞ comme limite, évidement!
et pour une suite qui n'a pas de limites... la plus connue est sans doute (-1)n et bientracez la fonction (-1)x sur vos calculettes et vous verrrez que la fontion oscille en permanence autour de l'axe des abscisses.
| critère de convergence |
|---|
Soit (un), (vn) et (wn) trois fonctions numériques vérifiant les trois conditions suivantes: |
Pour la petite histoire, ce théorème est appeléde théorème des gendarmes car on considère que les deux suites qui encadrent (vn) sont comme des gendarmes qui escortent un prisonnier vers le poste de police, ( en l'occurence, la limite des deux suites (un) et (wn)...
| Conséquence |
|---|
Soit un une suite numérique et L un nombre réel. |
je ne sais pas si vous vous rappellez de cette propriété des valeurs absolues que vous avez tous du voir au alentour de la 3ème ou de la seconde non?
| critère de divergence |
|---|
Soit (un) et (vn)deux suites numériques telles que (un)< ou = (vn) à partir d'un certains rang p (comme par hasard, toujours les mêmes lettres qui reviennent...):
|
Soit f ue fonction numériquedéfinie sur un intervalle ]a; +∞[ et (un) la suite définie pour tout entier supérieur à a, par un = f(n).
Si la fonction f admet en +∞, une limite finie , ou infinie, alors la suite (un) admet la même limite
Celà permet de résoudre pas mal d'exercice où l'on demande de calculer la limite d'une suite, en passant par la fonction, vous vous y reconnaissez quand même un peu, sinon, allez immédiatement ici
Les résultats concernats les opérations sur les limites de suites, sont analogues (c'est à dire identique) à celles que l'on a vu sur les limites de fonctions.
| Limites et opérations algèbriques |
|---|
Soient (un) et (vn) deux suites convergentes de limites respectives L et L'. Alors: |
Ba oui, après le magnifique chapite que l'on vient d'étudier, on ne peut pas ne pas en parler?!
| Limite d'une suite géométrique |
|---|
Soit q un réel non nul et différent de 1. |
Pfiou, c'était laborieux, en tout cas à rédiger... mais bon ce qui compte c'est que maintenant, les limites de suites numériques n'ont plus de secrets pour vous!!!