 Accueil
Accueil 
 Forum
Forum 
 Mail
Mail
OK, c'est bon, tout le monde est là? alors je continue mon cour mais avant laissez moi vous dire que ne pouvant placer des "petites flèches" au dessus des vecteurs je placerai l'attribut C.S.S. overline c'est a dire que les vecteurs seront uniquement marqués d'une ligne au dessus
OK, pas de problème mais c'est quoi un point pon... pond... pondéré?!
Je vous ai déjà dis, pas de panique, le monsieur Arn@Üde, il est là pour vous expliquer ce que vous ne comprenez pas OK?
Ba voilà, un point pondéré est un couple du type (A; α) où A est un point du plan ou de l'espace et α un nombre réel, c'est tout, vous allez voir par la suite pourquoi le réel &alpha est indispensable...
| définition |
|---|
| Soit (A; α) et (B; β) deux points pondérés du plan ou de l'espace, α + β ≠ 0. Il existe alors un unique point G qui vérifie la relation vectorielle: αGA + βGB = 0 G est alors barycentre des points pondérés (A, α) et (B, β) |
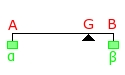
Une petite comparaison pour ceux qui ne comprennnent pas à quoi correspond concrètement un barycentre, imaginez vous que le réel α ou β soit une certaine masse suspendue aux extremités d'une tige sans masse, G définirait alors le point d'équilibre de la tige, pour qu'elle soit parfaitement horizontale.
Ce qui veut dire que le barycentre de deux points pondérés est obligatoirement situé sur la droite qui passe par ces deux points. Alors faïtes attention lros de vos constructions, pas d'inepties
Le barycentre de deux points pondérés reste inchangé si l'on multiplie les deux coeficient par un même nombre non nul
Vous allez pas tarder à savoir à quel point c'est utile lors de démonstrations, ce qui consituera ou a constitué l'escenciel de vos exercices sur ce chapitre
Ouvrez grand vos yeux et vos oreilles, enfin surtout vos yeux!
| Théorème |
|---|
| Si G est le barycentre de (A, α) et (B, β), avec α + β ≠ 0, alors pour tout point M, αMA + βMB = (α + β)MG |
Si le plan (ou l'espace) est muni d'un repère d'origine O et que dans la relation vue précédement, on remplace M par αOA + βOB = (α + β) OG, c'est à dire: OG = α/(α + β)OA + β/(&alpha + β)
Mais ce qui vous interresse, c'est les coordonnées de G,non ? alors voilàcomment on fait pour obtenir les coordonnées du barycentre de deux points pondérés:
| Définition |
|---|
| (A, α), (B, β), (C, γ) étant trois points pondérés, avec α + β + γ ≠ 0, il exits eun unique point G qui vérifie la relation vectorielle: αGA + βGB + &gammaGC G est alors le barycentre des points pondérés (A, α), (B, β), (C, γ) |
La propriété d'homogénéité étudiée pour deux points pondérés, est encore vraie pour trois points pondérés, à savoir, on ne change pas un barycentre, en multipliant tous les coéfficients par un même nombre non nul. Celà m'amène à vous dire tout de suite que en fait, cette partie est à peu de choses près la même que la précédente et donc vous allez voir un certains nombre de propriétés restent inchangées, ou sont modifiées uniquement dans le but de prendre en compte les trois points, là où il y en avait deux
Ainsi le baycentre de trois points pondéré se situe obligatoirement dans l'espace définie par ces trois points
| Théorème |
|---|
| Si g estle barycentre des ponts pondérés (A, α), (B, β) et (C, γ), avec α + β + γ ≠ 0 alors pour tout point m on a : αMA + βMB + γMC = (α + β + γ) MG |
Le calcum des coordonées du barycentre étudiées dans le cas de deux points s'adaptent au cas de trois points... à vous de les déduire attention, c'est cré cré cré difficile!!! mdr
J'attire votre attention sur ce paragrpahe qui est très important... et en plus pas dur du tout!!! ne me faîtes pas croire que vous n'êtes pas du genre "moins-j'en-fait-mieux-j'me-porte"
Soit G le barycentre des points pondérés (A, α), (B, β) et (C, γ) avec comme d'habitude α + β + γ ≠ 0
Si α + β ≠ 0, et si K est le barycentre (appelé barycentre partiel) de (A, α) et (B, β), G est alors encore le barycentre de (K, α + β) et (C, γ).
Soit n un entier naturel avec 2 ≤ n.
On peu généraliser la notion de barycentre à n points pondéré, où n est aussi grand que l'on veut
| définition |
|---|
| (A1, α1), (A2, α2),...,(An, αn) sont n points pondérés, avec α1 + α2+...+αn ≠ 0Il exitse un unique point G tel que : α1GA1 + α2GA2 +...+ α nGAn = 0 G est le barycentre de ces n points pondérés. |
Si les coefficients sont tous égaux et non nuls, G est l'isobarycentre de tous ces points.
Pour deux points, l'isobarycentre est le milieux du segment formé par ces deux points et pour trois points, on trouve le centre de gravité du triangle qu'ils forment
Encore une bonne nouvelle, les propriétés pour deux ou trois points pondérés sont encore vraies pour n points pondérés:
- propriété d'homogénéité;
- reduction de sommes vectorielles;
- calculs de coordonnées;
- barycenre partiel quand n est supérieur ou égal à trois
Les différentes transformations que vous connaissez (symétrie, translations, rotations) "conservent les milieux" qui est un cas particulier de barycentre...
f désigne une symétrie, une translation ou une rotation.
L'image G(f) du barycentre G de (A1, α1), (A2, α2),...,(An, αn) est le barycentre de (f(A1), α1), (f(A2), α2),...,(f(An), αn).
Encore un chapitre de plus qui s'achève, en général ce chapitre est apprécié des élèves car pas trop dur et de plus, on peut s'appuyer sur pas mal de schémas, ce que je vous conseille de faire lors de vos tests futurs pour ceux à qui ça ne serait pas venu à l'esprit...