Accueil Forum Mail Livre d'OR

Chapitres

NOMBRES DERIVES

I- Limite en a

Durant cette partie, je vous recommanderais toute votre attention car ce n'est pas vraiment facile à comprendre et que ceux qui aiment les formules compliquée se réjouisse, en voilà quelques unes et pas des plus amusantes.

Bon ok j'arrête de vous écœurer; alors commencer par retenir que dans cette partie, on va considérer un fonction f, définie sur un intervalle I (pour changer un peu quand même de temps en temps, mais on va rajouter une condition pour dire que l'intervalle I n'est pas réduit au seul réel a.
Ca va encore?

1) notion intuitive de limite finie de f(x) quand x tend vers a

Ouhais, prends moi pour un *** ! genre c'est intuitif ton truc là!!!!

Mais laissez-moi finir ... ah ces jeunes de nos jour, ils n'ont aucun respect!

Soit f une fonction définie sur un intervalle I, contenant la réel a sauf éventuellement en a, vous me suivez encore? Alors voilà, on dit que f tend vers l lorsque x tend vers a pour dire que les valeurs de f(x) sont aussi proche de l qu'on le souhaite, dès que x est suffisamment proche de a. Ou encore que la distance de f(x) à l peut être rendue inférieur à n'importe quel nombre positif a dès que les valeurs de f(x) sont suffisamment voisine de a.

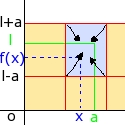On écris lim_{x -> a}f(x) = l

Je vais vous demandez de retenir quelque chose qui pourra vous être utile , à savoir que toutes les fonctions polynômes, quotients de polynômes, racine carrée, irrationnelles, valeur absolue, trigonométriques, sont telles que
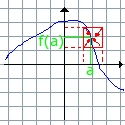
si f est définie en a, sa limite est f(a)

exemple 1	contre-exemple 2

1. lim_{x -> a} f(x) = f(a). On dit que f est continue en a.
2. f est définie en a, mais ne possède pas de limite en a:
   f n'est pas continue en a.

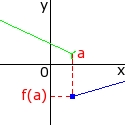Mais "kekispace" quand f n'et pas définie en a?

Soit a un réel d'un intervalle i et deux fonctions; f définie sur I sauf en a et g définie sur I.
Si g a une limite en a et si, pour tout réel x de I différent de a, on a f(x) = g(x), alors la limite de f(x) lorsque x tend vers a est g(a).
On écrit lim_{x -> a} f(x) = g(a)

II- définition du nombre dérivé de f en a

h étant un réel tel que a + h est un élément de i,
si h est différent de 0, le quotient (f(a + h)- f(a)) / h est ce que l'on appelle l'accroissement moyen de f entre a et a + h;
on parle aussi du taux d'accroissement de f entre a et a + h.
Si on pose x = a+h, l'accroissement moyen de f entre a et x (qui sont deux valeurs différentes) s'écrit:

(f(x) - f(a)) / (x - a)

Définition:

La fonction f est dérivable en a si et seulement si, la limite en 0 de ((f(a+h) - f(a)) / h) existe et est finie, c'est à dire que c'est un nombre qui ne dépend pas d'une variable.
Cette limite est le nombre dérivé de f en a et est notée f'(a)

f est dérivable en a <=> lim_{h -> 0} ((f(a + h) - f(a)) / h = f'(a)

En posant a + h = x, lorsque h tend vers 0, alors x tend vers a; donc :
f est dérivable en a <=> lim_{x -> a} ((f(x) - f(a)) / (x - a)) = f'(a).

Interprétation graphique du nombre dérivé de f en a

Cf est la représentation graphique de la fonction f dans un repère R, A est le point de Cf d'abscisse a et M le point d'abscisse a + h. pour h différent de 0, le quotient (f(a + h) - f(a)) / h est le coefficient directeur de la droite [AM]. la mesure 1 sur la figure est égale à f(a + h) - f(a)
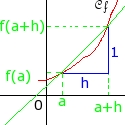Si la fonction f est dérivable en a, alors le coefficient (f(a + h) - f(a)) / h admet pour limite f'(a) lorsque h tend vers 0. Graphiquement, le point M se rapproche du point A et la droite (AM) tend à occupe une position limite la droite d. La droite d est tangente à la courbe Cf en A. la distance 2 est ici égale à h.f'(a)

TANGENTE
Si f est une fonction dérivable en a, le nombre dérivé de f en a est le coefficient directeur de la tangente à la courbe Cf au point A d'abscisse a Cette tangente a donc pour vecteur directeur, u (1 ; f'(a)).

Interprétation numérique du nombre dérivé de f en a

Soit une fonction f dérivable en a et sa courbe représentative cf.
A et M sont les point de cf d'abscisse a et a + h.
Pour h différent de 0, on pose :ð(h) = ((f(a +h) - f(a)) / h) - f'(a)
Si h tend vers 0, alors (f(a + h) - f(a)) / h tend vers f'(a).
Donc en additionnant ð(h) tend vers 0, on en déduit:
si f est dérivable en a, on peut écrire, pour h tel que a + h soit dans I:
f(a + h) = f(a) + hf'(a) + hð(h), avec lim_{h -> 0} ð(h) = 0

THEOREME
Soit f une fonction définie sur un intervalle i et a un réel de cet intervalle. Une fonction f est dérivable en a de nombre dérivé f'(a) signifie que:Il existe un réel ß et une fonction ð qui rend vers0 quand h tend vers 0 tels que pour tout réel h vérifiant a + h appartient à I, on a : f(a + h) = f(a) + hf'(a) + hð(h) et ß = f'(a).