Accueil Forum Mail Livre d'OR

Chapitres

Les fonctions numériques

I- RAPPEL

Bon, je suppose que vous savez tous ce qu'est une fonction, mais ça ne coute rien de faire un petit rappel, histoire de mettre tout le monde à l'aise!

Une fonction est un outil mathématique (entre autre) et qui associe à tout réel d'un interval, un seul réel.

notez que j'insiste sur la fait qu'une fonction n'associe un seul réel y à un réel x

on note: f(x)=y, ce qui se "traduit" par on applique la fonction f au réel x, ce qui nous donne le réel y.

voici un exemple de fonction: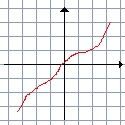

ex: f(x)= 3x+5 dans le cas ou x=3, on a alors f(3)=3×3+5, soit f(3)= 14

II- SENS DE VARIATION

Bon je pense que jusque là vous me suivez encore! On va donc attaquer une desième partie, à asvoir, l'étude du sens de variation d'une fonction.
Mais qu'est ce que le sens de variation?
on appelle si variation tout simplement le fait que la fonction soit croissante(quand elle monte) ou decroissante (quand elle descend) sur un interval donné.

Afin d'illustrer cette partie, nous nous servrons d'une fonction que l'on va appeler f et cette fonction sera défini sur un intervalle I.

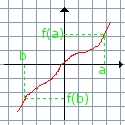	On dit que f est croissante sur I, lorsque, quels que soient les réels a et b appartenant a I , et pour a < b, on a f(a)<f(b) on dit également que les images respectives de a et b par f sont dans le même ordre que a et b
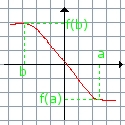	On dit que f est décroissante sur I, lorsque, quels que soient les réels a et b appartenant a I , et pour a < b, on a f(a)>f(b) on dit également que les images respectives de a et b par f sont dans l'ordre inverse de a et b

on verra plus tard que l'on peut regrouper les variations de f dans un tableau dit tableau de variations (ça doit vous surprendre!)

III- NOTION DE MINIMUM ET DE MAXIMUM

Maximum et minimum de f

On dit que le maximum de f sur un interval I (bien évidement choisi au hasard!) est le points de la courbe le plus élevé de cet interval.

on dit que f présente un maximum f(x_a) en A sur I quant on a : f(x)< ou = f(x_a)

vous l'auriez deviné, le minimum de f est le point le plus "bas" sur sa courbe representative: on dit que:

f présente un minimum f(x_b) en b si et seulement si on a f(x)> ou = f(x_b)

je n'ai pas résisté à la tentation du p'tit schéma...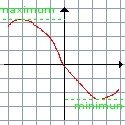

on voit que le maximum est le point le plus 'haut' de la courbe et que le minimum est au contraire le plus 'bas'

le maximum et le minimum sont ce que l'on appelle les extremmum (ou extremma) de f.

Majorée, minorée, bornée

je ne vais pas trop m'attarder sur ces notions car elles reprennent quaziment ce que je viens de vous expliquer, à savoir le maximum, le minimum et donc les extremmums d'une fonction.

• En effet, dire que f est majoré par M sur un certain interval revient à dire que f(M) est le maximum de f sur cet interval.
• De même dire que f est minoré par m sur I revient à dire que f(m) est le minimum de f sur cet interval.
• Et on dit qu'une fonction est bornée par deux nombres quand les variations de cette fonction sont comprises entre ces deux nombres.

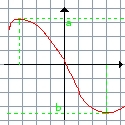On dit que f est majoré par a, minoré par b et donc bornée par a et b.

IV- Parité & periodicité

parité

Encore des noms compliqués pour des notions excessivement simples

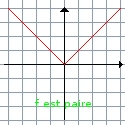	On dit qu'une fonction est paire quand sa représentation graphique admet un axe de symétrie.
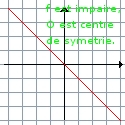	De même, une fonction est impaire quand sa représentation graphique admet un centre de symétrie

• une fonction est paire si et seulement si -x est défini quand x est défini et si l'on a f(x) = f(-x)

• et donc une fonction est impaire si f(-x) est défini et s'il on a f(-x) = -f(x)

Périodicité

Oulala j'entends déja les "keskecéksa?!"

Ba le "sa" c'est la manière "math" de dire que la reprédentation graphique de f admet une sorte de "motif" qui revient de façon récurente.vous allez tout de suite comprendre avec ce petit schéma:

je me permet toutefois de vous faire remarquer que le nombrel t que vous apercevez sur le schéma est un nombre qui est obligatoirement positif. Ce qui n'est pas dur a comprendre car en quelque sorte, il exprime la "distance entre chaque "motif" dont je vous parlais tout à l'heure.

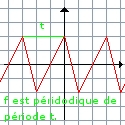
Comme vous deviez vous en doutez, il existe une formule mathématique pour démontrer qu'une fonction est périodique. Et cette formule, la voilà:

pour tout X, on a x + t appartient à l'ensmble de définition de la fonction , et l'on a f(x) = f(x+t) où T est ce que l'on appelle la période de la fonction

V- 3 exemples de fonctions usuelles

la fonction affine

RAPPEL:La fonction affine est une fonction qui a x associe le réel ax+b où a et b sont deux réel.
Alors trois cas de figure se présentent à nous:

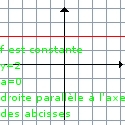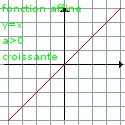
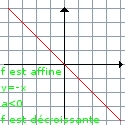
1er cas: a > 0 la fonction est croissante	2éme cas: a < 0 la fonction est décroissante	3ème cas: a = 0 la fonction est constante*

*dire qu'une fonction est constante est une fonction de la forme y = k ou k est i, réel, sa représentation graphique est une droite prallèle à l'axe des abcisses

la fonction carré

RAPPEL: la fonction carré est la fonction qui a x associe x²

• elle est défini sur l'ensemble des réels
• on a x²= (-x)² donc la fonction carré est paire
• Sa représentation graphique est une parabole qui a pour sommet l'origine du repère et pour équation y=x²
• elle est décroissante sur ]-∞, o] et croissante sur [0,+∞[

la fonction racine carré

RAPPEL: la fonction carré est la fonction qui a x associe la racine carré de x

• la fonction racine carré est défini sur [o;+∞[ car on ne peut pas prendre la racine d'un nombre négatif
• sur cet interval la fonction racine carré est croissante

---