Accueil Forum Mail Livre d'OR

Chapitres

PRODUIT SCALAIRE

I- Produit scalaire dans un repère orthonormal

On travaille dans le plan avec un repère orthonormal (O;i; j); les vecteurs u et v ont respectivement pour coordonnées (x;y) et (x';y')..

Produit scalaire

Définition:
Le produit scalaire de deux vecteurs u et v est le nombre noté u.v et qui est égale à :xx' + yy'

Ainsi le carré scalaire du vecteur u est u.u = u² = x² + y². Or vous savez que ||u||² = x² + y², vous en avez déduit que ||u||² = u².

Voilà encore une formule comme on les aime tant....

u.v = 1/2 [ ||u +v||² -||u||² - ||v||² ]

Vecteur orthogonaux

Soit O, A et B 3 points tels que u = OA et v= OB.

1. Les vecteurs u et v sont orthogonaux veut dire que
   • soit u = 0 ou v = 0
   • soit (OA) et (OB) sont perpendiculaires, à conditions toutefois que les vecteurs u et v soit différent de 0.
   
   
   
2. Théorème: 2 vecteurs sont orthogonaux, à condition que leur produit scalaire soit nul, c'est à dire que:
   - u.v = 0
   - ou encore(xx' +yy') =0
   
   
3. On dit que deux droites D et D' sont orthogonales si leurs vecteurs directeurs u et v sont orthogonaux
   soit si u.v = 0.

Propriétés du produit scalaire

Vous avez remarquer j'en suis sur le "s" au mot propriété dans le titre.... ba oui que croyez-vous, on est là pour bosser! euh.... Quoi pourquoi vous me regardez comme ça?! j'ai dit quelque chose que je n'aurais pas du dire??? xD

Ok, alors on va commencer molo! On va partir de trois vecteur que , à tout hasard, je vais appeler u, v et w ( et arrêter de dire que je n'ai pas d'inspiration! :P. On va également se servir d'un réel quelconque qui sera appelé k.

A partir de là, on distingue deux propriétés:

1. symétrie >>> u.v = v.u
   
   
2. linéarité >>> u.(v + w) = u.v + u.w
   de même >>> .(kv) = k(u.v)
   
   
3. Produit scalaire de deux vecteurs colinéaires u et v:
   Si les vecteurs sont colinéaire, c'est qu'il existe un réel a tel que u = av, il en résulte deux cas de figure:
   • si a > 0 ( les deux vecteurs sont de même sens), alors u.v = ||u|| × ||v||.
   • si a < 0 ( les vecteurs sont alors de sens contraire), alors, u.v = -||u|| × ||v||.

Égalités remarquables

BONNE NOUVELLE pour vous, les identités remarquables des produits scalaires ressemblent étrangement à celle que vous connaissiez déjà avec les fameux a² et b²!!! C'est à dire que:

- (u + v)² = (u + v).(u + v) = u² + 2u.v + v².

- ||u + v||² = ||u||² + ||v||² + 2u.v

- (u - v)² = (u - v) (u - v) = u² + v² - 2u.v

- ||u - v||² = ||u||² + ||v||² - 2u.v

- (u + v) . (u - v) = u² - v²

- (u + v) . (u - v) = ||u||² - ||v||².

II- Définition géométrique du produit scalaire

Produit scalaire et angles : théorème
u et v sont deux vecteurs non nuls et l'angle (u; v) = α, alors, on a : u.v = ||u|| ||v|| cos α.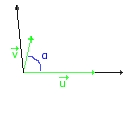

Voilà encore un de mes supers schémas qui a le mérite d'être claire et concis (c'est le moins que l'on puisse dire!!!

Une série de remarques qui s'imposent d'elles-mêmes...

- si α = 0 alors les vecteurs sont colinéaires u.v = ||u|| × ||v||;
- si α = π , c'est à dire que les vecteurs sont de sens contraires; alors u.v = - ||u|| × ||v||;
- si les vecteurs sont orthogonaux ( si &alpha: = ±π) alors u.v = 0.

Rien de bien sorcier là dedans!!! si vous avez du mal à comprendre ça, rvd ici!!!

Produit scalaire et projeté orthogonaux

Un petit rappel, c'est quoi un projeté orthogonal???
On appelle projeté orthogonal d'un point sur une droite, le point d'intersection de la perpendiculaire à cette droite passant par ce point et de la droite elle-même? Vous ne voyez pas?! ok alors re schéma...

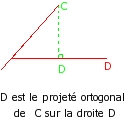
Voilà maintenant ce qu'il faut retenir:

Les points A B et C sont distincts et je vais appeler H le projeté orthogonale de C sur (AB). Alors on a :
AB.AC =

--> AB × AH Si les vecteurs sont de même sens ou
--> - AB #215, AH Si les vecteurs sont de sens contraires

De même, AB.AC = AK.AC si K est le projeté orthogonal de B sur la droite (AC)

Projeté orthogonal d'un vecteur

On considère le projeté orthogonal v₁ de v sur un axe (A, i), où i est unitaire. v₁ est colinéaire à i. Il existe donc un réel X tel que v₁ = Xi et on a i.v = i.v₁ = Xi² = X car on a dit plus haut que i est le vecteur unitaire

définition

Soit un axe (A; i), où i est un vecteur unitaire, et v un vecteur non nul.Le projeté orthogonale de v sur l'axe (A, i) est le vecteur v₁ = (i.v)i.

En élargissnt ce que je viens de dire , on peut en déduire que si un vecteur v a pour coordonnées X et Y dans un repère orthonormal (O, i, j), alors on a X = i.v et Y = j.v.

Propriétés

Encore le "s" au mot propriété, ce "s" que vous commencez à appréender...

On va parler d'une droite d; de A qui sera un point de d, de n(a, b) un vecteur normal à la droite d et c un réel

1. Pour tout point M de d, on a AM.n = 0
2. Si la droite d admet n pour vecteur normal, alors d a pour équation ax + by + c = 0
3. toute droite d'equation ax + by + c = 0 admet n(a, b) pour vecteur normal

III- Propriétés numériques

1) Théorème de la médiane

Soit A et B deux points et I le milieu de [AB], pour tout point M on a : MA² + MB² = 2MI² + 1/2 AB² MA² - MB² = 2MI².BA MA.MB = MI² - IA²

2) relation métrique dans un triangle

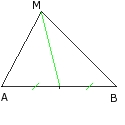Soit a, b et c des réels strictement positif, ABC est un triangle tel que BC = a, AC = b et AB = c Théorème de AL-KASHI: a² = b² + c² - 2 bc × cos (A) b² = c² + a² - 2 ca × cos (B) c² = a² + b² - 2 ab × cos (C)

(A) signifie l'angle du triangle en A soit ici l'angle (CAB), je suis désolé de vous dire que je ne sais pas comment on fait les "petits chapeaux" au-dessus des angles alors je me contente de les mettre entre ( ). Vous avez les excuses d'Arn@Üde, pour ce qu'elles valent...

Comme on se retrouve

ABC est un triangle rectangle en A, alors (A) = π/2et cos(A) = 1, on retrouve alors le théorème le plus connu du monde, elui de Pythagore car no obtient dans ce cas, c² = a² + b²

3) formule des sinus

Soit ABC un triangle non aplati, dont l'air est S, on a alors:

• S = 1/2 bc× sin(A) = 1/2ca × sin(B) = 1/2ab × sin(C)
• et a/(sin(A)) = B/(sin(B)) = C/(sin(C)) = abc / 2S